Data Assimilation
1. Data Assimilation
The main problem that is considered is how to correct our understanding of measurements done in the presence of noise. Given certain quantities like a measurement from a sensor, a distribution from which the process generates data, or new measurements after the first, we ask ourselves, how can we combine all given information into a calculation.
2. Ikeda Map Example
In this example, we consider the Ikeda map. It is a discrete dynamical system governed by:
\begin{align} x_{n + 1} &= 1 + u (x_{n} \cos(t_{n}) - y_{n} \sin(t_{n})) \\ y_{n + 1} &= u(x_{n} \sin(t_{n}) + y_{n} \cos(t_{n})) \end{align}Where \( u \) is some parameter and
\[ t_{n} = 0.4 - \frac{6}{1 + x_{n}^{2} + y_{n}^{2}} \]
2.1. Preamble
import jax import flax import jax.numpy as jnp from jax import jit from jax import lax import matplotlib.pyplot as plt import seaborn as sns sns.set() key = jax.random.key(0) key, subkey = jax.random.split(key)
2.2. Implementation
We can implement this very easily in JAX or TensorFlow. For now I will be using JAX as I have a bit of a crush on the software at the moment.
@jit def ikeda_update(point): u = 0.9 x, y = point[...,0], point[...,1] t = 0.4 - (6 / (1 + x ** 2 + y ** 2)) x_new = 1 + u * (x * jnp.cos(t) - y * jnp.sin(t)) y_new = u * (x * jnp.sin(t) + y * jnp.cos(t)) return jnp.stack((x_new, y_new), axis=-1) ikeda_jacobian = jit(jax.jacfwd(ikeda_update)) @jit def iterate(points): def body_fn(i, val): return ikeda_update(val) return lax.fori_loop(0, 50, body_fn, points) @jit def generate_ikeda(subkey, size=10**5): return iterate(jax.random.uniform(subkey, shape=(size, 2), minval=0, maxval=0.5)) %timeit generate_ikeda(subkey) key, subkey = jax.random.split(key) def plot_ikeda_points(points = []): """ Plots extra given points against an ikeda background Points is a list(tuple(x,y,color)) """ attractor = generate_ikeda(jax.random.key(0)) plt.scatter(attractor[:3000, 0], attractor[:3000, 1], label='Attractor Points') for point in points: plt.scatter(**point) plt.legend(bbox_to_anchor=(1,1)) return None plot_ikeda_points()
21.5 ms ± 385 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)
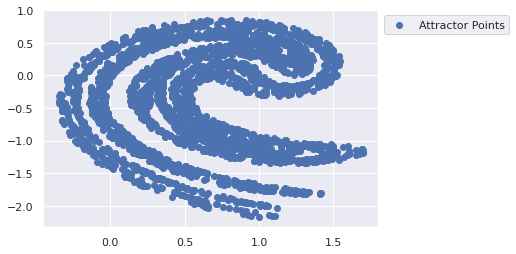
2.3. State Estimation Visualization
First, suppose we have a green point on the attractor that we want to track.
from matplotlib.animation import FuncAnimation time_units = 10 true_state = jnp.array([1.25, 0]) fig, ax = plt.subplots(1,1) attractor = generate_ikeda(subkey) class ikeda_attractor: def __init__(self, true_state : jax.numpy.array): self.true_state = true_state def update(self, i): return None def animate(i): global true_state ax.clear() ax.scatter(attractor[:3000, 0], attractor[:3000, 1], label='Attractor Points') ax.scatter(*true_state, label='True State') true_state = ikeda_update(true_state) anim = FuncAnimation(fig, animate, frames=time_units, interval=50) plt.show()
Suppose
2.4. Measurement Problem
Now that we have a green point to track, suppose that we only have a measurement device at the origin which can measure the distance (like a RADAR device).
# Prior state estimate: \hat{x}^{-} true_state = jnp.array([1.25, 0]) # Prior covariance: P^{-} prior_covariance = 1/16 * jnp.eye(2) prior_estimate = true_state + 1/4 * jax.random.normal(subkey, shape=(2,)) key, subkey = jax.random.split(key) # Nonlinear Measurement 'h' @jit def measure(true_state): return jnp.linalg.norm(true_state) # Measurement Covariance: r measurement_covariance = jnp.array([1/4]) # Measurement: y = h(x) + eta measurement = measure(true_state) + jnp.sqrt(measurement_covariance) * jax.random.normal(subkey) key, subkey = jax.random.split(key)
First let us see how the system evolves.
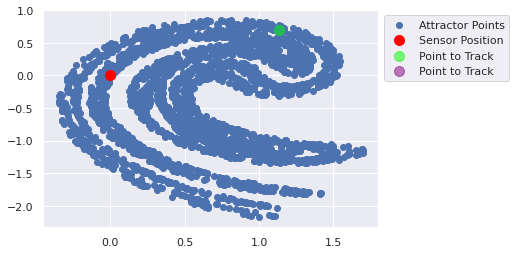
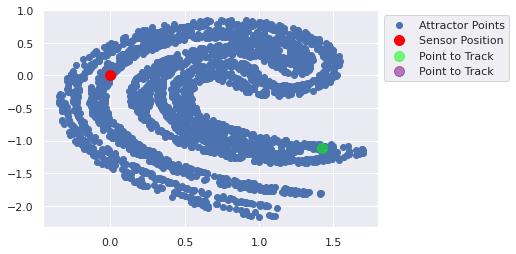
def track_point(time_units, true_state, prior_estimate, prior_covariance, update_method, update_method_kwargs): """ Given a starting (true) point, a prior estimate of the state, a prior covariance of the state, a """ for time_unit in range(time_units): plot_ikeda_points([ {'x':0,'y':0,'c':'red','label':'Sensor Position','s':100}, {'x':true_state[0],'y':true_state[1],'c':'lime','label':'Point to Track','s':100, 'alpha':0.5}, {'x':prior_estimate[..., 0],'y':prior_estimate[..., 1],'c':'purple','label':'Point to Track','s':100, 'alpha':0.5}, ]) plt.show() true_state = ikeda_update(true_state) print(prior_estimate) prior_estimate, prior_covariance = update_method(prior_estimate, prior_covariance, **update_method_kwargs) track_point(time_units=10, true_state=jnp.array([1.25, 0]), prior_estimate=jnp.array([1.25, 0]), #+ jax.random.uniform(minval=-0.1, maxval=0.1, key=key, shape=(100,2)), prior_covariance=jnp.eye(3), update_method=lambda x_1, x_2, **x: (ikeda_update(x_1)+ 0.01, x_2), update_method_kwargs={})
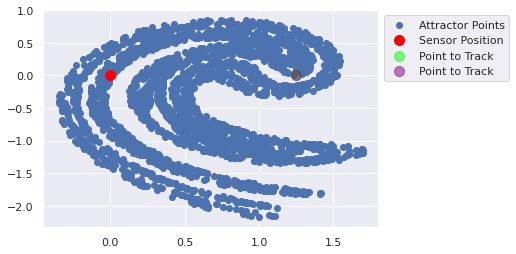
[1.25 0. ]
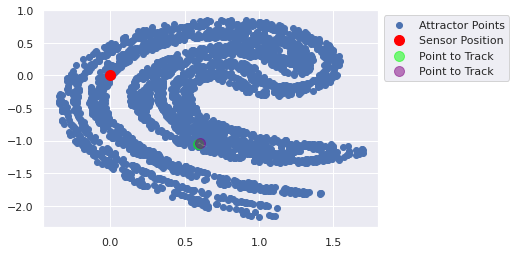
[ 0.6024831 -1.0385966]
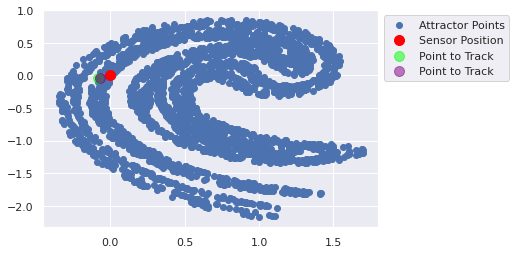
[-0.06979907 -0.03225724]
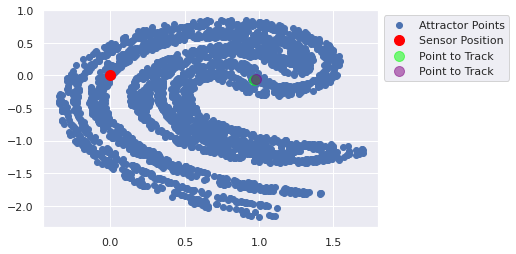
[ 0.98181725 -0.05320451]
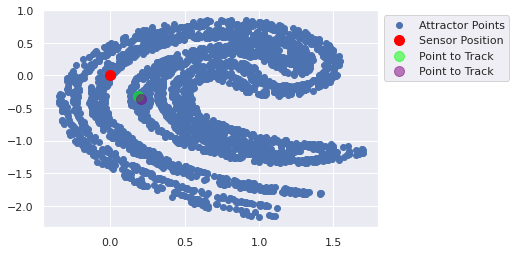
[ 0.20815751 -0.3643704 ]
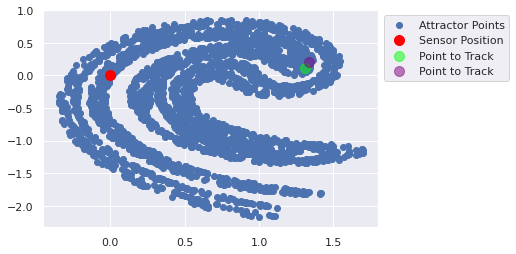
[1.3358982 0.20086011]
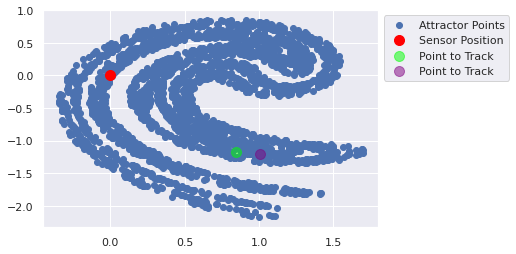
[ 1.0052788 -1.2058134]
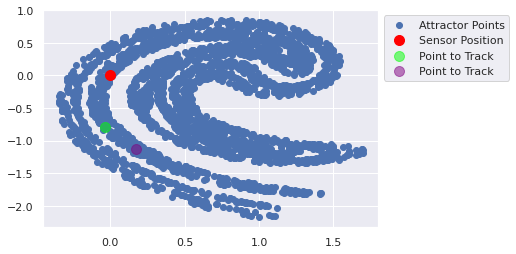
[ 0.16977595 -1.1259253 ]
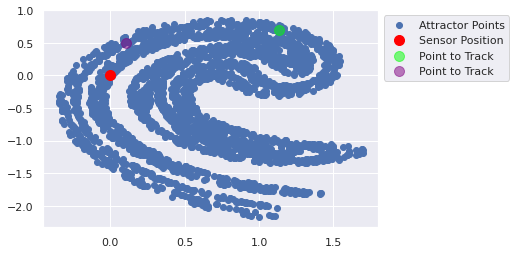
[0.10684864 0.4942605 ]
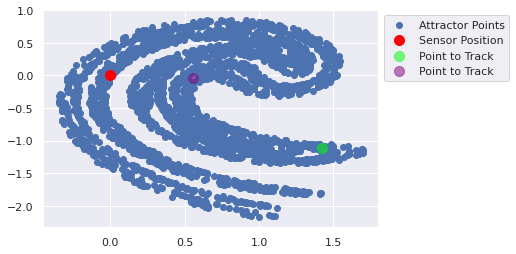
[ 0.5582348 -0.04507566]
2.5. Measurement
Now that we have a green point which we want to follow, we now construct a new estimate, a purple point,
2.6. Bayesian Recursive Update
def bayesian_recursive_update(prior_estimate, prior_covariance, measurement, measurement_covariance, num_steps): state_estimate = prior_estimate covariance = ikeda_jacobian(prior_estimate) @ prior_covariance @ ikeda_jacobian(prior_estimate).T measurement = prior_estimate for _ in range(num_steps): measurement_jacobian = jax.grad(measure)(state_estimate) kalman_gain = covariance @ measurement_jacobian.T * (measurement_jacobian @ covariance @ measurement_jacobian.T + num_steps * measurement_covariance) ** (-1) state_estimate = state_estimate + kalman_gain * (measurement - measure(state_estimate)) covariance = (jnp.eye(2) - kalman_gain @ measurement_jacobian) @ covariance print(state_estimate) return state_estimate, covariance track_point(time_units=10, true_state=jnp.array([1.25, 0]), prior_estimate=jnp.array([1.24, 0]),# + jax.random.uniform(minval=-0.1, maxval=0.1, key=key, shape=(100,2)), prior_covariance=jnp.eye(2), update_method=bayesian_recursive_update, update_method_kwargs={'measurement':measure(jnp.array([1.25, 0])), 'measurement_covariance':measurement_covariance, 'num_steps':20})
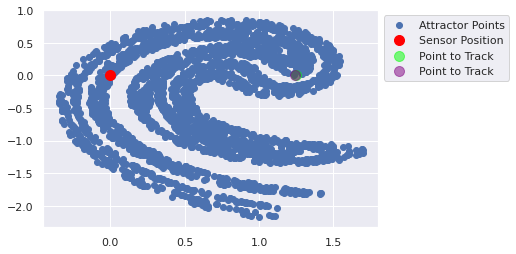
[1.24 0. ][1.1314527 1.3454187]
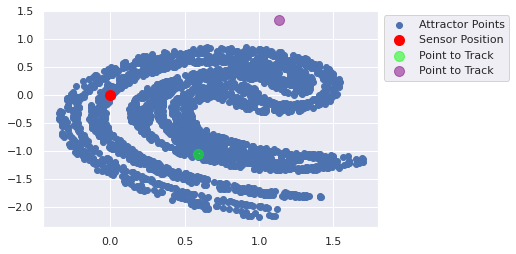
[1.1314527 1.3454187] [ 0.8926025 -0.91010994]
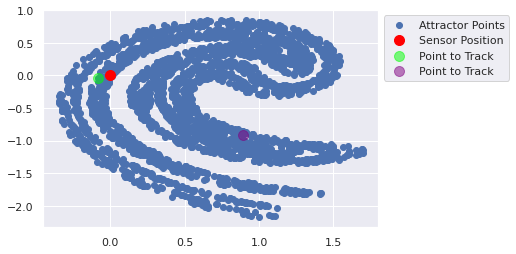
[ 0.8926025 -0.91010994] [0.6987301 0.01448113]
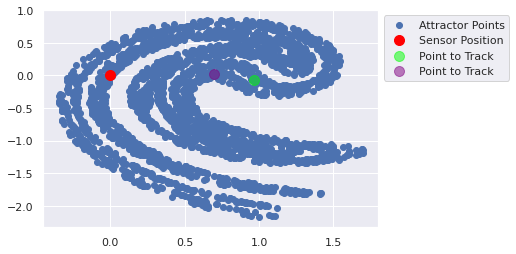
[0.6987301 0.01448113] [779.3692 267.2606]
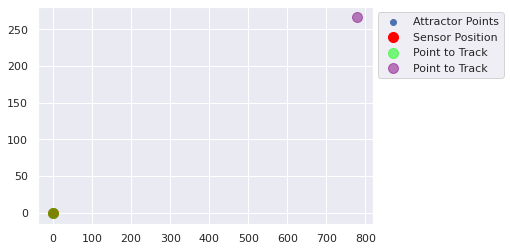
[779.3692 267.2606] [108752.64 108246.95]
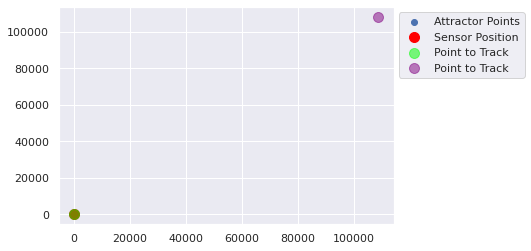
[108752.64 108246.95] [97646.51 47751.188]
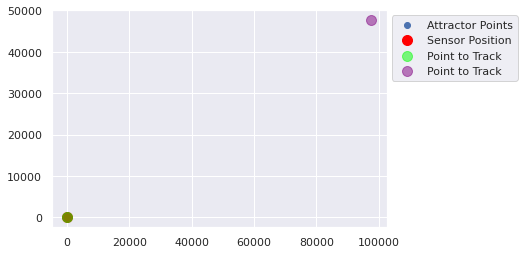
[97646.51 47751.188] [nan nan]
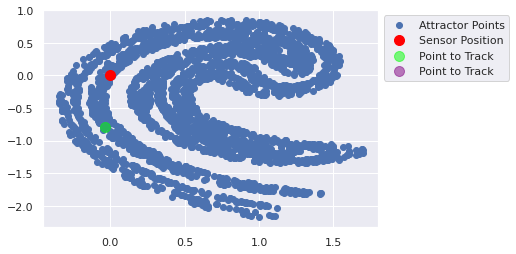
[nan nan] [nan nan]
[nan nan] [nan nan]
[nan nan] [nan nan]
2.7. Test
#key, subkey = jax.random.split(key) #ensemble = jnp.array([1.25, 0]) + jax.random.uniform(minval=-0.5, maxval=0.5, key=key, shape=(100,2)) #ensemble.mean(axis=0) jnp.linalg.inv(jnp.array([[2]])) def func(x1, x2): pass func(**{'x1':1, 'x2':2})